在分布式系统中,数据复制是提高系统可用性和性能的重要手段。然而,数据复制也带来了多副本数据一致性的问题。为了在性能和一致性之间找到平衡,分布式系统采用了一系列一致性模型。本文将从数据复制的场景出发,探讨一致性模型的重要性、定义以及常见的一致性模型,并通过具体示例说明每种模型的特点和应用场景。
1. 为什么需要一致性模型?
分布式系统要保证系统的可用性以及性能,就需要对数据提供一定的冗余度:分布式系统实现上常用的方法是复制 (replication) 和分片 (sharding)。而我们将要讨论的一致性模型 (consistency model),主要是与复制有关。
同一份数据保存在多个机器上提供冗余度,也被称为副本(replica)策略,这个做法带来下面的好处:
- 可用性:通过多副本机制,即使某个副本不可用,系统仍可以通过其他副本继续提供服务。例如,MySQL的主备同步方案就是典型的例子。
- 性能:通过数据复制,可以将请求分流到多个副本,从而提高系统的吞吐量。此外,在地理分布上,数据复制可以通过就近原则提高客户端访问数据的效率。例如,CDN技术就是通过数据复制实现高效内容分发的典型应用。
同时,副本策略也有自己需要解决的问题,其中最重要的问题就是一致性问题:在系统中的一个机器写入的数据,是否在系统中其他机器看来也是一样的?换句话说就是我们希望在其中一个副本上所做的修改,在其它副本上也能随时观察到(即读取到)。
很显然,即便在一切都正常工作的条件下,在系统中的一个机器成功写入了数据,因为广播这个修改到系统中的其他机器还需要时间,那么系统的其他机器看到这个修改的结果也还是需要时间的。换言之,中间的这个时间差可能出现短暂的数据不一致的情况。
在实际使用的时候,我们并不需要去关心所有时刻的数据一致性的情况,我们关心的是当我们每次去观察的时候(读取数据的时候),系统所表现出来的是否是一致的 ,即使系统内部出现了短暂的不一致的情况,但是在对外表现出来的数据是一致的,就可以了。
在最理想的情况下,整个分布式系统应该表现得像一个 “单一的副本” 一样即“单一系统视图”,使用者不需要思考分布式系统内部的复杂性,仅仅依靠单体系统的经验就能以较简单的方式来使用这个系统。
为了解决一致性问题,需要首先定义一致性模型,在维基的页面上,一致性模型(Consistency model)的定义如下:
In computer science, a consistency model specifies a contract between the programmer and a system, wherein the system guarantees that if the programmer follows the rules for operations on memory, memory will be consistent and the results of reading, writing, or updating memory will be predictable.
我们举一个日常生活中常见的问题来解释一致性模型:
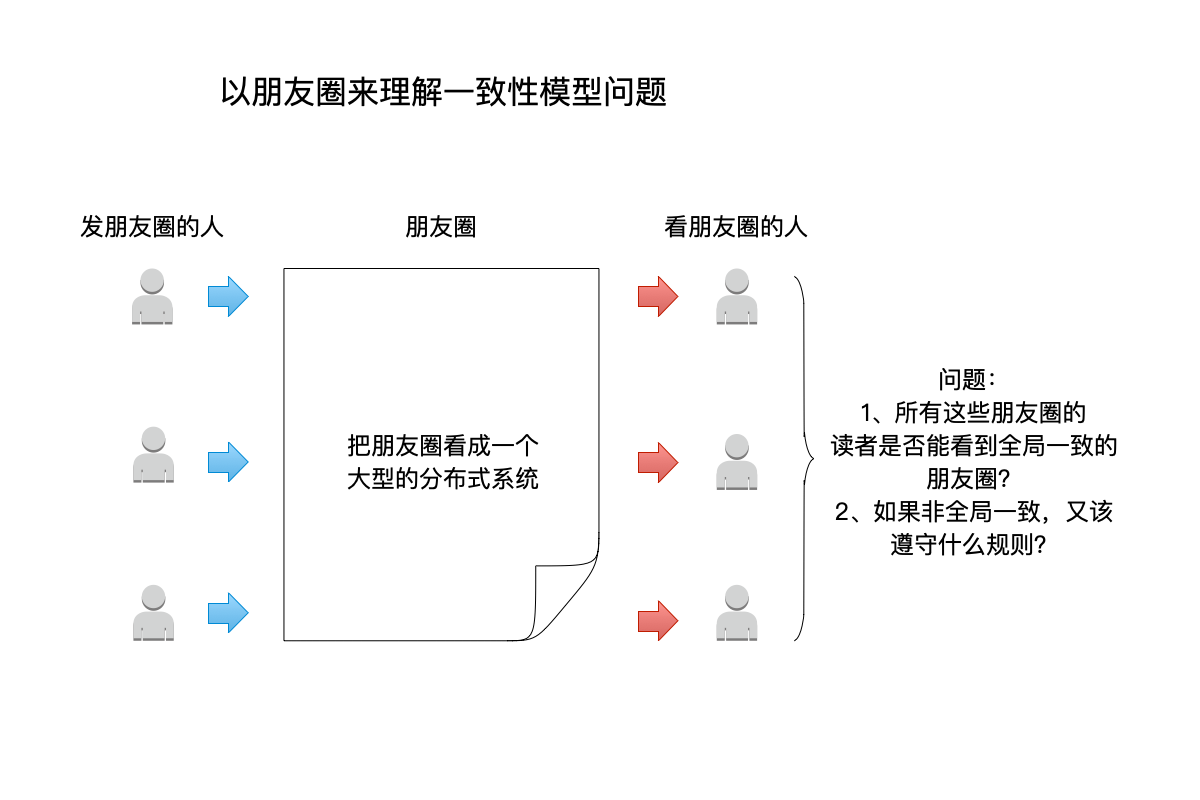
在上图中:
- 不妨把
朋友圈当成一个大型的分布式系统:- 这个分布式系统,对外提供了写入(发朋友圈)和读取( 读朋友圈)的功能。
- 存储这些朋友圈数据的,肯定不止一台机器,因此这些机器在一起构成了这个大型的分布式系统。
- 不同的用户,发朋友圈的时候,也不一定都写入相同的一台机器。反之也是,在读朋友圈时也不一定会到同一台机器上读取数据。
朋友圈这个分布式系统,有两种客户端:发朋友圈的客户端负责写入数据,读朋友圈的客户端负责读取数据,当然很多时候同一个客户端既能读也能写。
接下来的问题是:
- 这些看朋友圈的人,是否能看到全局一致的数据?即所有人看到的朋友圈都是同一个顺序排列的?
显然,有很多时候,即便是在看同一个朋友圈下的评论回复,不同的人看到也不尽然都是同一个顺序的,所以以上的答案是否定的。那么就引入了下一个问题:
- 如果不同的人看到的朋友圈(包括评论)顺序各有不同,这些顺序又该遵守怎样的规则才是合理的?
单进程下的事件排列
一条朋友圈下面有多个人发表评论,可以认为这是一个二维的数据:
- 进程(也就是发表评论的人)是一个维度。
- 时间又是另一个维度,即这些评论出现的先后顺序。
但是在阅读这些评论的读者看来,需要将这一份二维的数据,去除掉不同进程这个维度,压平到只有本进程时间线这一个单一维度上面来,以上面图例来说就是这样的:
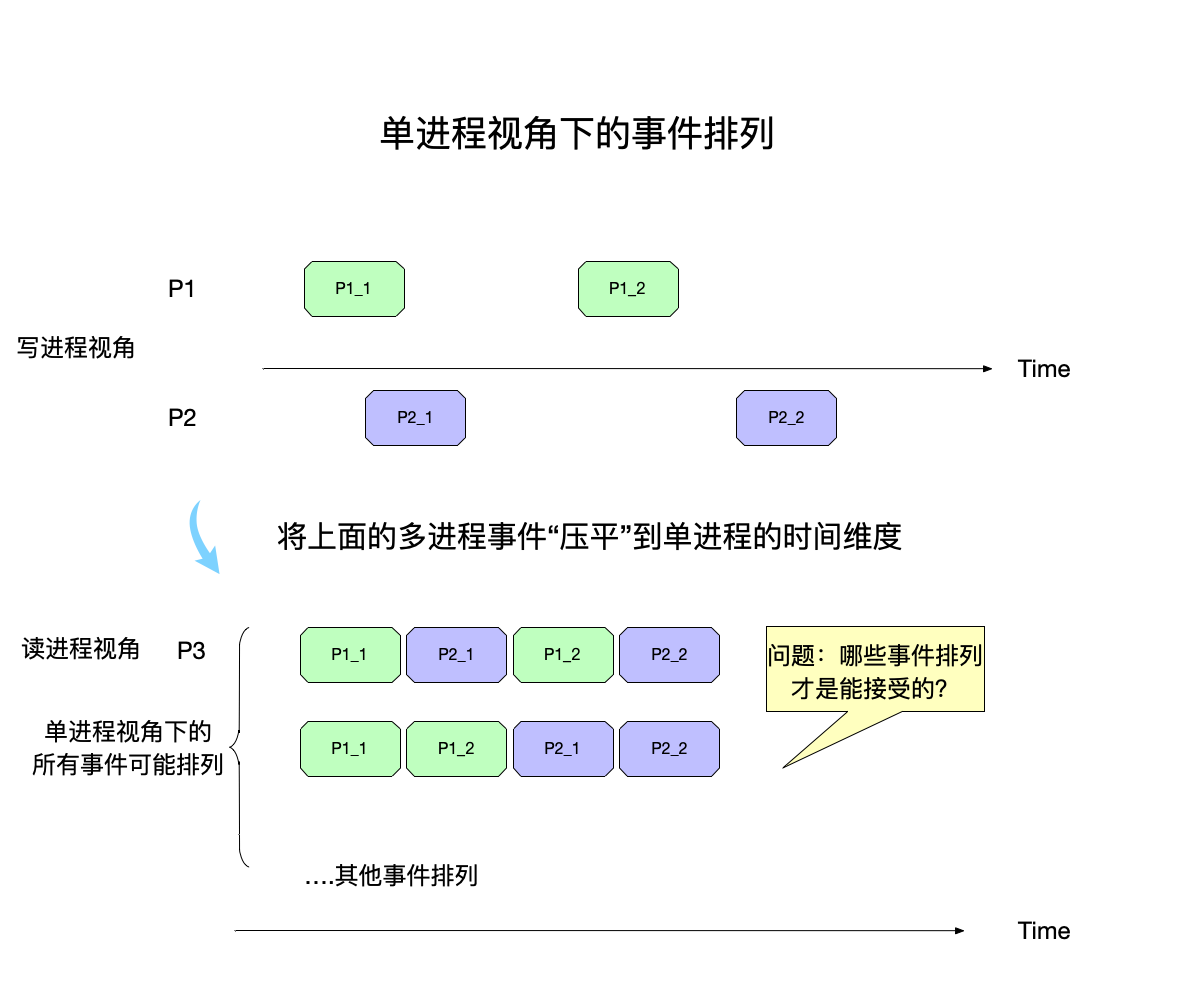
在上图中,在读进程P3P3的视角看来,两个写进程的事件,需要压平到本进程的时间线上进行排列,可以看到这些事件在压平之后有多种排列的可能性。
将多个写进程的事件进行排列,放到单进程的时间线上,这是一个排列组合问题,如果所有的写进程事件加起来一共有n个,那么这些事件的所有排列组合就是n!n!。比如事件a、b、c,不同的排列一共有这些:
{(a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a)}一致性模型就是要回答:在所有的这些可能存在的事件排列组合中,按照要求的一致性严格程度,哪些是可以接受的,哪些不可能出现?
越是宽松的一致性模型,能容纳的事件排列可能性就越多;反之越严格则越少。
一致性模型
一致性模型是进程与数据存储之间的约定:如果进程遵循某些规则,那么进程对数据的读写操作都是可预期的。
可以这么说,一个分布式系统对于读写操作的某种排序和执行规则,就定义了一种一致性模型 (consistency model)。当一个系统选定了某种特定的一致性模型(比如线性一致性或顺序一致性),那么你就只能看到这种一致性模型所允许的那些操作序列。
基本术语:
- 数据存储:分布式系统中的共享数据库、文件系统等。
- 读写操作:
- 写操作:包括新增、修改、删除等更改数据的操作。
- 读操作:读取数据的操作。
一致性模型定义了在多副本环境下,读写操作的行为和结果。例如:
- 强一致性模型:保证所有进程对数据的读写顺序一致。
- 弱一致性模型:允许一定程度的数据不一致,以提高系统性能。
强一致性模型
强一致性模型要求所有进程对数据的读写顺序保持一致。以下是两种常见的强一致性模型:
顺序一致性
顺序一致性的定义最初出现在论文《How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Progranm》中,原文中要求顺序一致性模型满足两个要求:
the result of any execution is the same as if the operations of all the processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by its program.
(任何执行的结果都与所有处理器的操作按某种顺序执行的情况相同,每个单独的处理器的操作按其程序指定的顺序出现在这个序列中。)
它有两个条件:
Requirement Rl: Each processor issues memory requests in the order specified by its program.
Requirement R2: Memory requests from all processors issued to an individual memory module are serviced from a single FIFO queue. Issuing a memory request consists of entering the request on this queue.
先来看条件1:
- 条件1:每个进程的执行顺序要和该进程的程序执行顺序保持一致。
前面提到过,当读进程读到多进程的多个事件时,相当于把这些不同时间、进程维度的事件“压平”到本进程的同一个时间维度里,条件1要求这样被压平之后的顺序,每个进程发出的事件的执行顺序,和程序顺序(program order)保持一致。
举一个违反这个条件的反例,如下图所示:
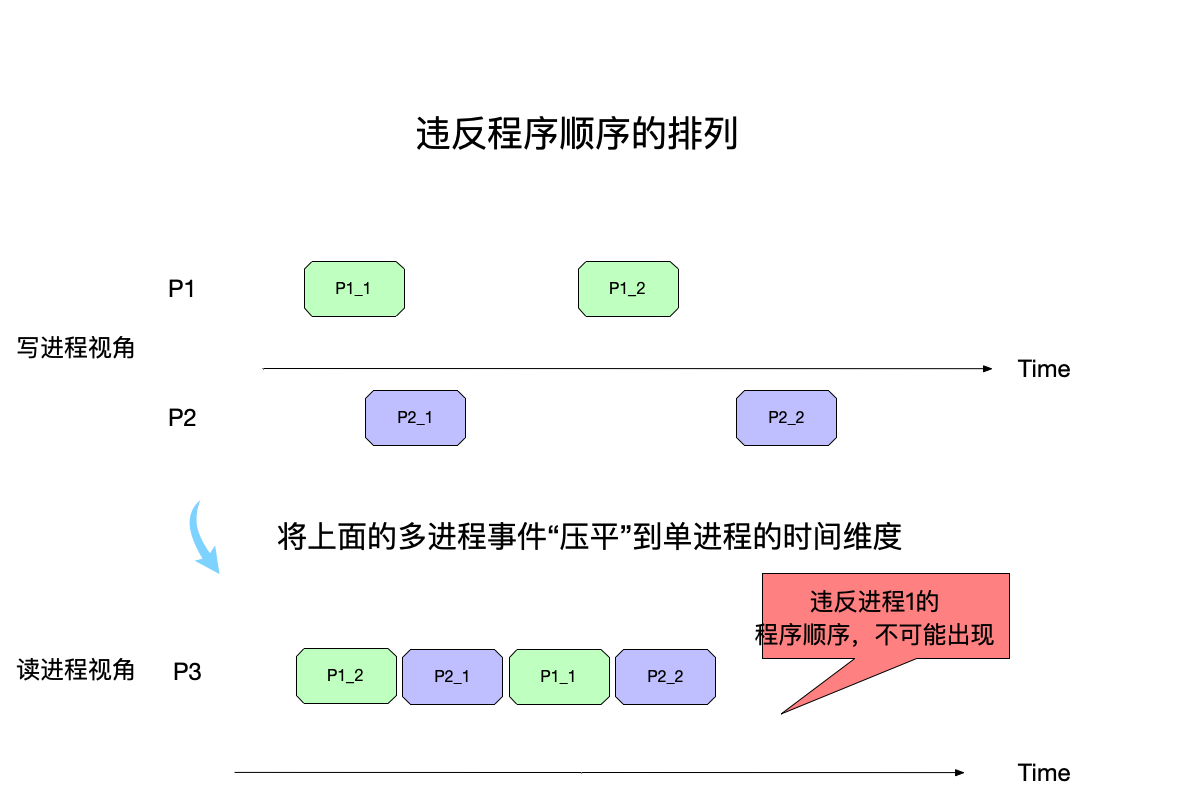
上图中:
- 进程P1P1视角下:程序的执行顺序是先执行 P11P11,再执行 P12P12。
- 但是到了P3视角下重排事件之后,P12P12出现在了事件P11P11前面,这是不允许出现的,因为违反了原进程P1P1的程序顺序了。
但是,仅靠条件1还不足以满足顺序一致性,于是还有条件2:
- 条件2:对变量的读写要表现得像FIFO一样先入先出,即
每次读到的都是最近写入的数据。
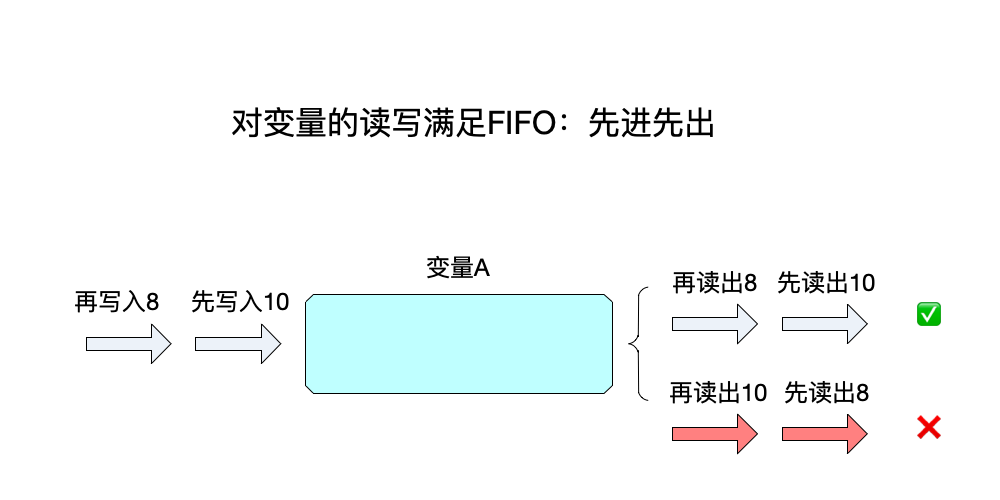
我们来举一个例子来完整说明顺序一致性:
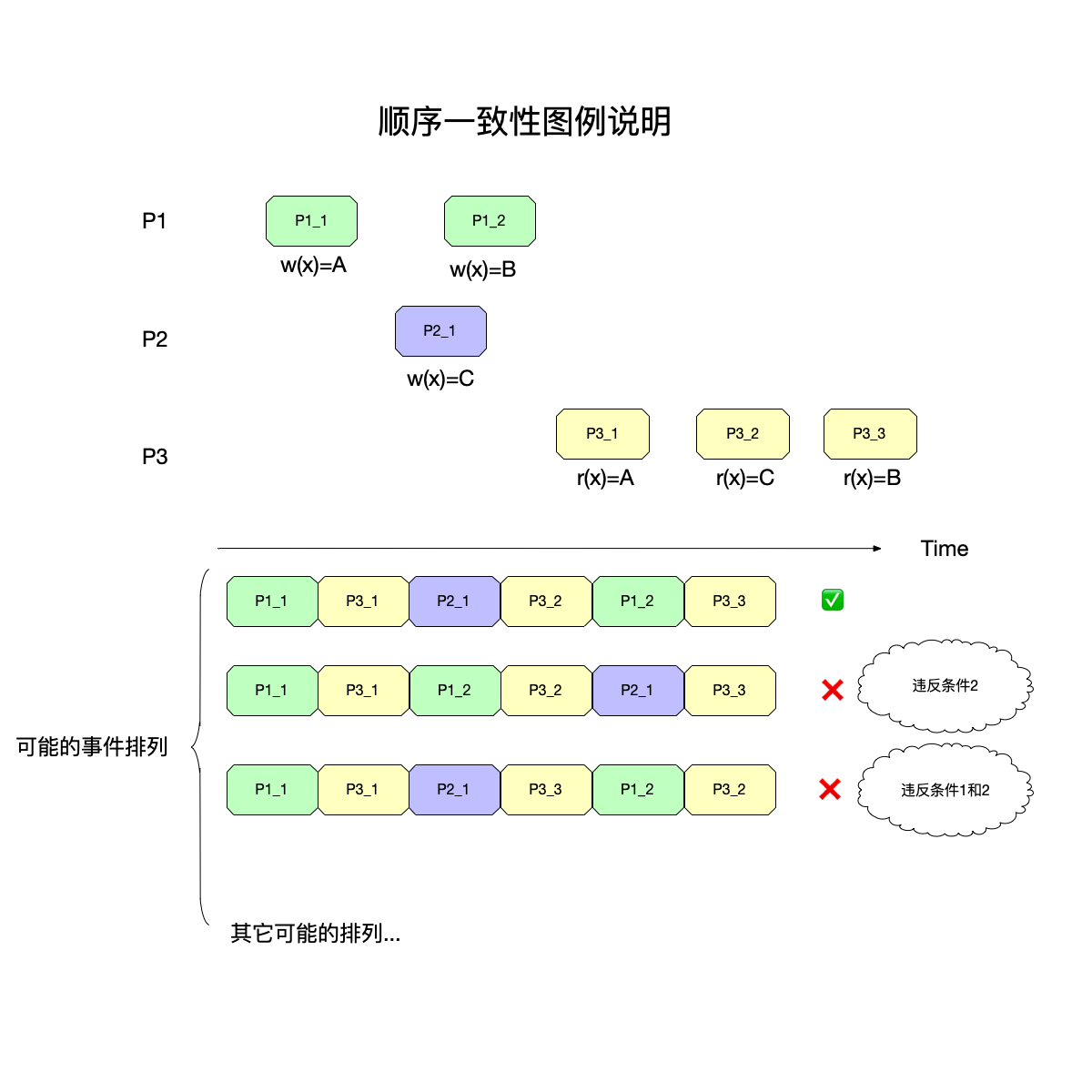
上图中,有三个进程对变量x进行读写操作:
进程P1P1:事件P11P11修改x为A,事件P12P12修改x为B。
进程P2P2:事件P21P21修改x为C。
进程P3P3:事件P31P31读出x为A,事件P32P32读出x为C,事件P31P31读出x为B。
注意:在上图中,事件P12P12和P21P21有重叠,意味着这两个事件是“并发事件”,即哪个事件先发生、完成都是可以接受的。
图中下半部分给出了三种可能的事件排列:
- 第一种排列:
- 将事件对应的操作解读出来,那么执行顺序为:{w(x)=A,r(x)=A,w(x)=B,r(x)=B,w(x)=C,r(x)=C}。
- 可以看到,上面这个顺序,既没有违反条件1(因为同进程的程序顺序没有被打乱),也没有违反条件2(读出的都是开始写入的数据)。
- 第二种排列:
- 将事件对应的操作解读出来,那么执行顺序为:{w(x)=A,r(x)=A,w(x)=B,r(x)=C,w(x)=C,r(x)=B}。
- 由于P12P12和P21P21是并发事件,可以任意排列两者的顺序,这里选择先执行P12P12,可以看到:
w(x)=B,r(x)=C,这违反了条件2。
- 第三种排列:
- 将事件对应的操作解读出来,那么执行顺序为:{w(x)=A,r(x)=A,w(x)=C,r(x)=B,w(x)=B,r(x)=C}。
- 这一次选择了先执行P21P21,可以看到:
w(x)=C,r(x)=B以及w(x)=B,r(x)=C:违反了条件2。- P33P33先于P32P32执行,违反了条件1。
以上就是顺序一致性的解释,它要求两个条件:
- 不能打乱单进程的程序顺序,同一个进程里的事件先后顺序要得到保留。
- 每次读出来的都是最新的值,而且一旦形成了一个排列,要求系统中所有进程都是同样的一个排列。
这里需要特别说明的是,只要满足这两个条件,并没有对不同进程的事件先后顺序其他硬性的规定,所以即便是某些事件在排列之后看起来违反了事件发生的先后顺序也是可以的。其实这在上图中已经有体现了:
- 事件P31P31明明比事件P12P12和P21P21发生得更晚,但是只要在重排之后它是紧跟着P11P11的第一个读事件,就没有违反顺序一致性。在这个大前提下,事件P31P31甚至能出现在P12P12和P21P21之前,这看起来就很
违反直觉了。
再比如下图:
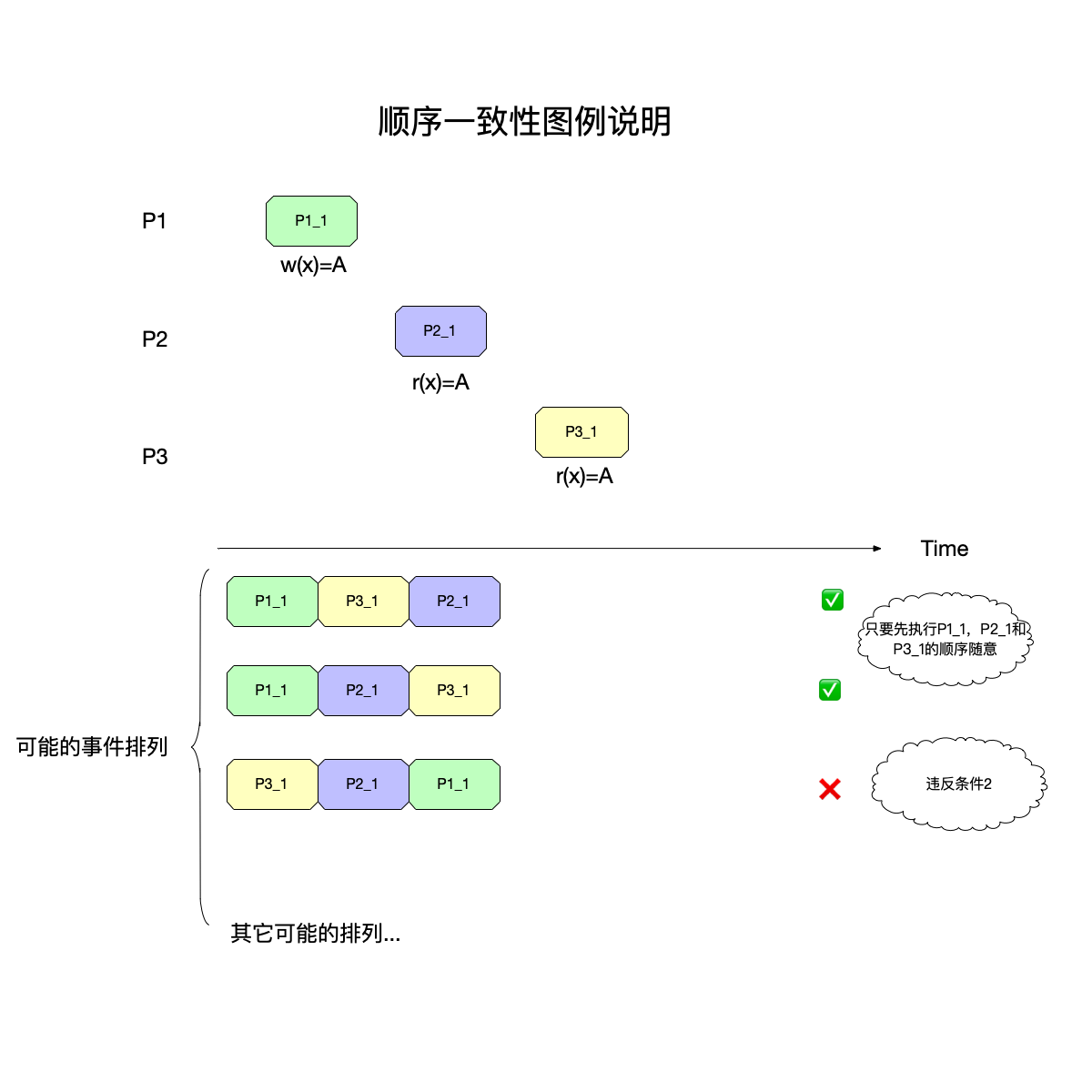
在上图中,故意将三个事件画的分开一些,意味着三个事件并不重叠,即有明确的先后顺序,但是在顺序一致性模型看来:
- {P11P11,P21P21,P31P31}和{P11P11,P31P31,P21P21}都是对的,因为这两者都没有违反条件1和2。
- 只有最下面的{P31P31,P21P21,P11P11}才是错的,因为违反了条件2。
可以看到,顺序一致性在满足了条件1、2之后,对不同进程的事件之间的顺序没有硬性的要求,即便在感官直觉上某事件应该发生得更早,但是只要没有违反这两个条件就可以认为是满足顺序一致性模型的。
于是就出现了更严格的线性一致性,它基于顺序一致性的条件,对事件的先后顺序做了更严格的要求。
线性一致性(linearizability 实际上,它就是CAP 定理中的C)
线性一致性要求首先满足顺序一致性的条件,同时还多了一个条件,不妨称之为条件3:
- 条件3:不同进程的事件,如果在时间上不重叠,即不是并发事件,那么要求这个先后顺序在重排之后保持一致。
如果加上这个更强的条件,上面的图中,就只有{P11P11,P21P21,P31P31}是满足线性一致性的排列了。
再举一个例子来说明线性一致性:
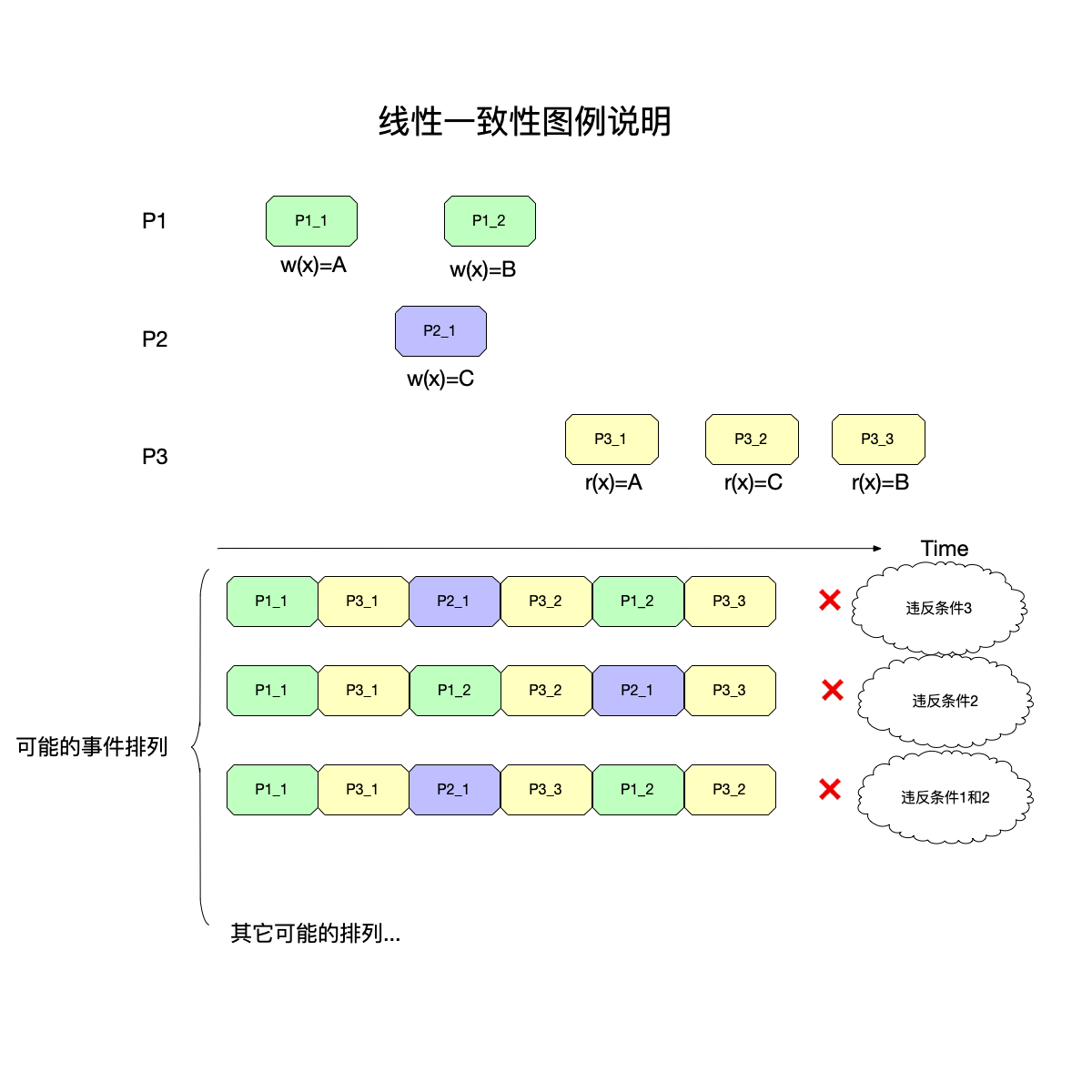
这还是最开始解释顺序一致性模型的图,但是在线性一致性的条件下,找不到能够满足条件的排列了。
这是因为:
- 事件P21和P12都在事件P11之后,这个顺序需要得到保持。
- 而事件P31在事件P21和P12之后,这个顺序也需要得到保持。
- 如果保持了前面两个顺序,那么P31执行的时候,必然读不出来A,而应该是B或者C(即P21或者P12的执行结果)。
顺序一致性和线性一致性总结
可以看到,如果满足线性一致性,就一定满足顺序一致性,因为后者的条件是前者的真子集。
除了满足这些条件以外,这两个一致性还有一个要求:系统中所有进程的顺序是一致的,即如果系统中的进程A按照要求使用了某一种排序,即便有其他排序的可能性存在,系统中的其他进程也必须使用这种排序,系统中只能用一种满足要求的排序。
这个要求,使得满足顺序和线性一致性的系统,对外看起来“表现得像只有一个副本”一样。
但因果一致性则与此不同:只要满足因果一致性的条件,即便不同进程的事件排列不一致也没有关系。
弱一致性模型
弱一致性模型通过放宽一致性要求,提高系统性能。以下是几种常见的弱一致性模型:
因果一致性
相较于顺序和线性一致性,因果一致性就简单一些,其实就只要满足在Lamport 逻辑时钟中提到的happen-before关系即可:
引入符号→→做为表示事件之间
happen-before的记号。在同一个进程中,如果事件a在事件b之前发生,那么a→b。(这是因为根据规则1,进程每次发出事件之后都会将本地的lamport时钟加一,于是可以在同一个进程内定义事件的先后顺序了)
在不同的进程中,如果事件a表示一个进程发出一个事件,事件bb表示接收进程收到这个事件,那么也必然满足a→b。(这是因为根据规则2,接收进程在收到事件之后会取本地时钟和事件时钟的最大值并且+1,于是发出事件和接收事件尽管在不同的进程,但是也可以比较其lamport时钟知道其先后顺序了)
最后,
happend-before关系是满足传递性的,即:如果a→b且b→c,那么也一定有a→c。
以评论朋友圈这个行为来解释因果一致性再合适不过:
- 评论另一个用户的评论:相当于进程给另一个进程发消息,肯定要求满足
happen-before关系,即先有了评论,才能针对这个评论发表评论。 - 同一个用户的评论:相当于同一个进程的事件,也是必须满足
happen-before关系才行。
以下图为例:
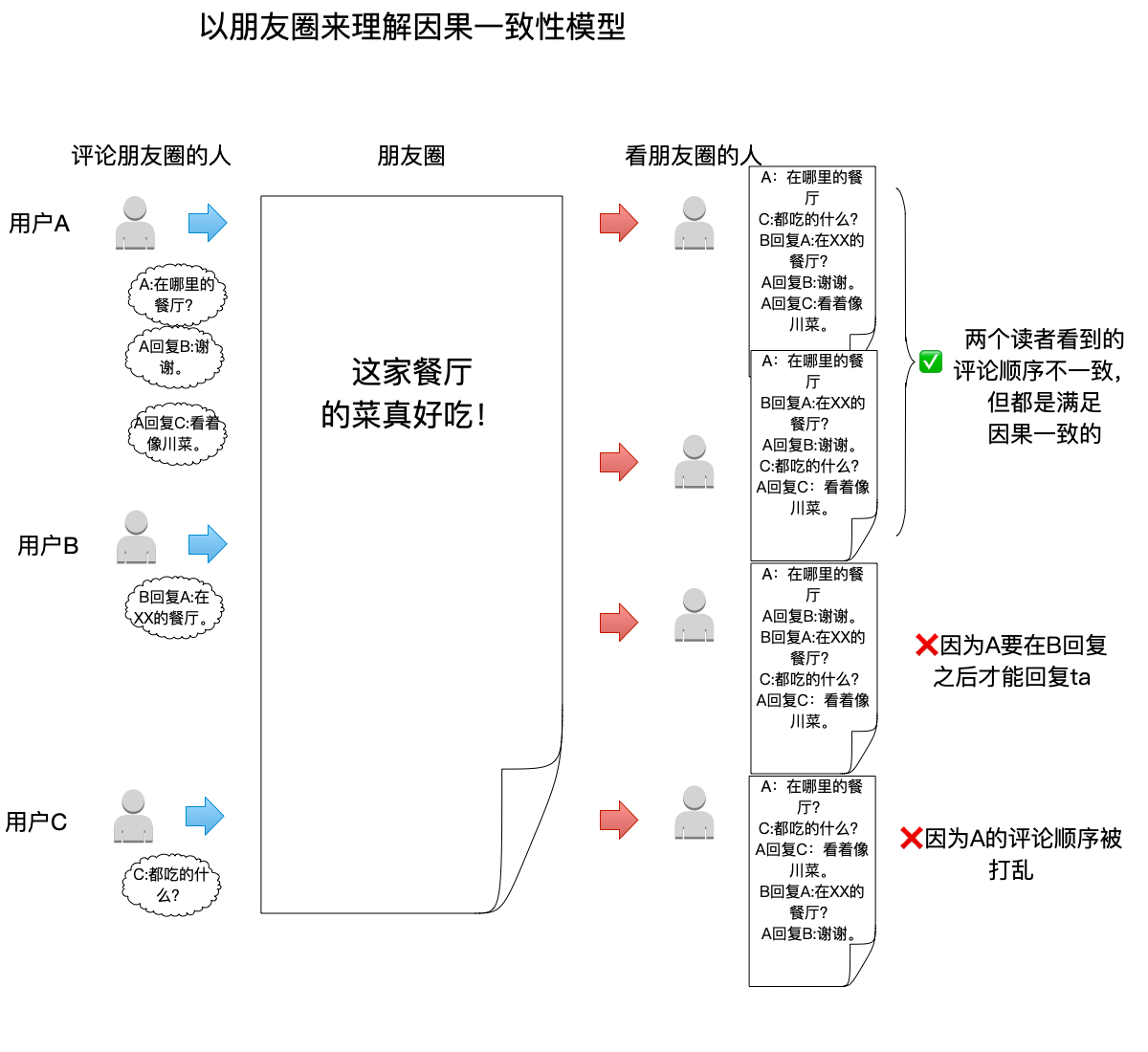
一共有4个朋友圈的读者,它们看到的评论顺序都各不一样:
- 最上面的两个读者,读到的顺序都满足因果一致性,因此即便是不一样的顺序也是正确的。
- 最下面的两个读者,顺序都不满足因果一致性:
- A回复B这个事件出现在了B回复A之前,不符合多进程之间的
happen-before关系。 - A回复C这个事件在进程A中应该在A回复B之前,不符合同一进程的事件之间的先后顺序。
- A回复B这个事件出现在了B回复A之前,不符合多进程之间的
最终一致性(Eventual Consistency 可以对应CAP 定理中的A)
根据CAP定理,当分布式系统中存在网络分区(Partition)时,系统必须在可用性(Availability)和强一致性(Consistency)之间进行取舍。此外,即使在没有网络分区的情况下,系统也需要在延迟(Latency)和强一致性之间进行权衡。这是因为维持强一致性需要付出额外的成本,一致性要求越强,系统的性能和延迟开销越大。
最终一致性(Eventual Consistency)是一种弱一致性模型,它的设计思路不再试图提供单一系统视图(SSI,Single System Image),即不再要求系统“表现得像只有一个副本”一样。相反,它允许系统在某一时刻存在数据不一致的情况,但保证在没有新的更新操作时,所有副本最终会达到一致状态。
最终一致性的原始定义出自Werner Vogels的论文《Eventually Consistent》(2008),其定义如下:
Eventual consistency. This is a specific form of weak consistency; the storage system guarantees that if no new updates are made to the object, eventually all accesses will return the last updated value.
最终一致性是弱一致性的一种特殊形式;存储系统保证,如果对象没有新的修改操作,那么所有的访问最终都会返回最新写入的值。
我们发现,虽然最终一致性和本文前面讨论的线性一致性或顺序一致性在命名上非常相似,但它的定义却与后两者存在非常大的差别。深层的原因在于,它们其实属于不同类别的系统属性 (property)。线性一致性和顺序一致性属于 safety property(安全性);而最终一致性属于 liveness property(活性)。
一个并发程序或者一个分布式系统,它们的执行所展现出来的系统属性,可以分为两大类:
- safety:它表示「坏事」永远不会发生。比如,一个系统如果遵守线性一致性或顺序一致性,那么就永远不会出现违反三个(对于顺序一致性来说是两个)条件的执行过程。而一旦系统出现问题,_safety_被违反了,我们也能明确指出是在哪个时间点上出现意外的。
- liveness:它表示「好事」最终会发生。这种属性听起来会比较神奇:在任何一个时间点,你都无法判定_liveness_被违反了。因为,即使你期望的「好事」还没有发生,也不代表它未来不会发生。就像最终一致性一样,即使当前系统处于不一致的状态,也不代表未来系统就不会达到一致的状态。而只要系统存在“在未来某个时刻达到一致状态”的可能性,最终一致性就没有被违反。另外,可用性 (availability) 也属于_liveness_属性。
通常来说,只有当_safety_和_liveness_这两种属性被同时考虑时,一个系统才能提供有意义的系统保证。而当系统设计者遵循最终一致性的设计思路时,相当于放弃了所有的_safety_属性。这意味着,对于系统使用者来说,你必须针对数据不一致的可能性做好补偿措施 (compensation)。但不管怎么说,最终一致性仍然被认为是系统提供数据一致性的最低要求。
最终一致性是最弱的一致性模型,其条件包括:
最终同步:所有副本的数据最终会在某个时刻保持一致。
时间范围:系统需要提供一个有下限的时间范围,保证数据最终一致。
允许读取旧数据:在数据同步完成之前,客户端可能会读取到旧版本的数据。
示例
假设有一个分布式数据库,客户端A在副本M上写入x=1,客户端B在副本N上写入x=2。在最终一致性模型下,系统最终会将x的值同步为2(假设以时间戳最新的数据为准)。但在同步完成之前,不同的客户端可能会读取到不同的值(如x=1或x=2)。
最终一致性的应用场景
社交网络:在社交网络中,用户发布的内容可以容忍短暂的不一致,最终一致性能够保证所有用户最终看到相同的内容。
内容分发网络(CDN):CDN通过最终一致性保证内容在不同节点之间的同步,优先保证内容的可用性和分发效率。
分布式缓存:分布式缓存系统通常采用最终一致性,以提高缓存的读写性能。
以客户端为中心的一致性(Client-centric Consistency)
以客户端为中心的一致性为单一客户端提供一致性保证,确保客户端在多次操作中能够看到一致的数据视图。其子模型包括:
1. 单调读一致性(Monotonic Read Consistency)
定义:保证客户端不会读取到旧值。即,如果一个客户端读取到某个数据的某个版本,那么它后续的读取操作不会返回比这个版本更旧的值。
示例:假设客户端A在副本M上读取
x=1,然后副本M宕机,客户端A连接到副本N。在单调读一致性模型下,客户端A在副本N上读取x的值仍为1,而不是旧值0。
2. 单调写一致性(Monotonic Write Consistency)
定义:保证客户端的写操作是串行的。即,一个客户端的写操作必须按照它们发生的顺序被其他客户端看到。
示例:客户端A先写入
x=1,再写入x=2。在单调写一致性模型下,其他客户端看到的x的值必须按照1到2的顺序更新。
3. 读写一致性(Read Your Writes Consistency)
定义:保证客户端能读取到自己最新写入的值。即,一个客户端在写入某个数据后,后续的读取操作必须能够看到这个写入的结果。
示例:客户端A写入
x=1后,立即读取x的值,必须得到1,而不是旧值。
4. 写读一致性(Writes Follow Reads Consistency)
定义:保证客户端的写操作基于其最新读取的值。即,一个客户端在读取某个数据后,后续的写操作必须基于这个读取的结果。
示例:客户端A读取
x=1后,写入y=2(y的计算依赖于x的值)。在写读一致性模型下,y=2必须基于x=1的结果。
以客户端为中心的一致性的特点
适用于单一客户端:以客户端为中心的一致性主要为单一客户端提供一致性保证,确保客户端在多次操作中能够看到一致的数据视图。
弱一致性模型:与强一致性模型相比,以客户端为中心的一致性模型对系统的要求较低,适用于对一致性要求不高的场景。
应用场景
用户会话管理:在分布式系统中,用户的会话数据需要保证单调读一致性和读写一致性,以确保用户在不同节点上看到的数据是一致的。
分布式缓存:在分布式缓存系统中,以客户端为中心的一致性可以保证客户端在多次读取操作中不会看到旧数据。
总结
在分布式系统中,多个进程组合在一起协调工作,产生多个事件,事件之间可以有多种排列的可能性。
一致性模型本质上要回答这个问题:按照该一致性模型定义,怎样的事件排列才符合要求?
顺序一致性和线性一致性都意图让系统中所有进程
看起来有统一的全局事件顺序,但是两者的要求不同,顺序一致性:- 条件1:每个进程的执行顺序要和该进程的程序执行顺序保持一致。
- 条件2:对变量的读写要表现得像FIFO一样先入先出,即每次读到的都是最近写入的数据。
只要满足这两个条件,顺序一致性对事件之间的先后顺序并没有硬性要求,而线性一致性在此基础上多了条件3:
- 条件3:不同进程的事件,如果在时间上不重叠,即不是并发事件,那么要求这个先后顺序在重排之后保持一致。
因果一致性是更弱的一致性,只要满足
happen-before关系即可。由于happen-before关系实际上是由Lamport时钟定义的,这是一种逻辑时钟,所以不同的读者看到的先后顺序可能会有点反直觉,但是只要满足happen-before关系就是正确的。
Reference:
分布式系统一致性的发展历史 (一)条分缕析分布式:浅析强弱一致性 - 铁蕾的个人博客
 YJ
YJ